Corrigé du 10 P. 405

retour

Notons respectivement $S_i$, $P_i$ et $T_i$ les événements « le $i$-ième élève tiré est en seconde, première ou terminale ».

On peut (éventuellement) modéliser la situation par l'arbre ci-dessous

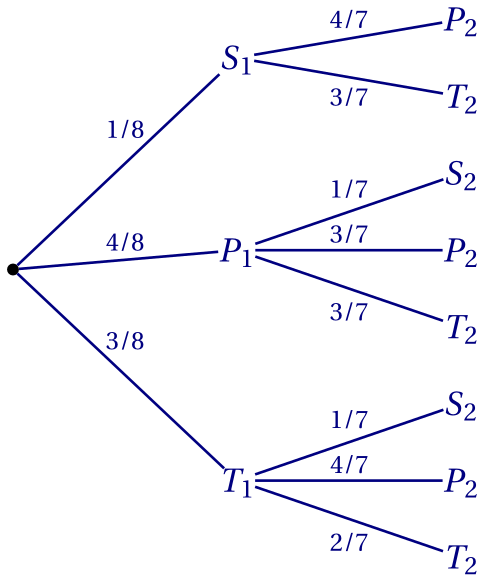
Alors la probabilité cherchée est: \begin{align*} p &= P(P_1 \cap P_2) + P(T_1\cap T_2)& \\ &= P(P_1) \times P_{P_1}(P_2) + P(T_1)\times P_{T_1}(T_2)& \\ &= \frac 4 8 \times \frac 3 7 + \frac 3 8 \times \frac 8 7& \\ &= \frac 3 {14} + \frac 3 {28}& \\ &= \frac{6+3}{28}& \\ &=\frac 9 {28}.& \end{align*}

On pouvait aussi utiliser le dénombrement:

Il y a $\displaystyle\binom{8}{2}=28$ tirages possibles de deux élèves parmi 8, tous équiprobables.
Parmi ces tirages $\displaystyle\binom{4}{2}=6$ comportent deux élèves de première et $\displaystyle\binom{3}{2}=3$ comportent deux élèves de terminale.
Donc \[p = \frac{6+3}{28} = \frac{9}{28}.\]

retour