Corrigé du 11 P. 405

retour

a. Il y a 3 jours sur 7 dont le nom contient la lettre A. Lorsque l'on choisit un jour au hasard, on a donc une probabilité égal à $\dfrac 3 7$ de tomber sur un jour avec la lettre A.
Notons $A_i$ l'événement « le $i$-ème jour tirée a un nom contenant la lettre $A$ ». Alors l'arbre pondéré est le suivant:

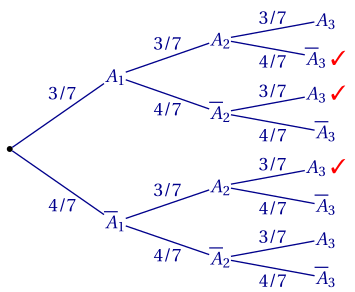
b. Trois parcours dans l'arbre mènent à exactement deux jours avec un A. \begin{align*} &P(A_1 \cap A_2 \cap \overline A_3) + P(A_1 \cap \overline A_2 \cap A_3) + P(\overline A_1 \cap A_2 \cap A_3)& \\ = &\frac 3 7 \times \frac 3 7 \times \frac 4 7 + \frac 3 7 \times \frac 4 7 \times \frac 3 7 + \frac 4 7 \times \frac 3 7 \times \frac 3 7& \\ = &3 \times \frac{36}{343}& \\ = &\frac{108}{343}.& \end{align*}

retour