Corrigé du 12 P. 407

retour

1. On lance à chaque fois la même pièce (expériences identiques) et chaque résultat de lancer n'influence pas les suivants (expériences indépendantes).
C'est donc bien un schéma de Bernoulli.

2. Si l'on note $A_i$ l'événement «le $i$-ème lancer à donné "pile"», on peut réaliser l'arbre suivant:

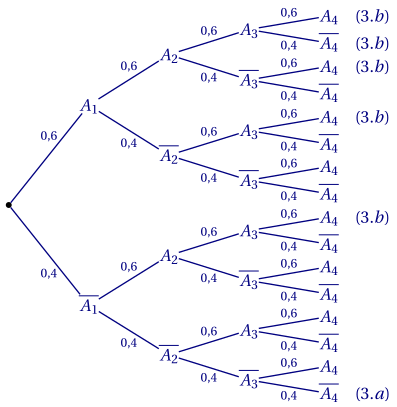
3.a. Un seul parcours dans l'arbre correspond à quatre fois "face": \[\overline{A_1}\cap\overline{A_2}\cap\overline{A_3}\cap\overline{A_4}.\] Sa probabilité est donc \[0,4^4 = 0,0256.\]

3.b. On peut avoir soit trois "piles", soit quatre "piles". La probabilité est donc: \[0,6^4 + 4\times 0,6^3\times 0,4 = 0,1296 + 0,3456 = 0,4752.\]

retour