Corrigé du 48 P. 418

retour

1. En notant respectivement $R_i$ et $B_i$ les événements «la $i$-ème boule tirée est rouge/bleue», on peut construire l'arbre suivant.

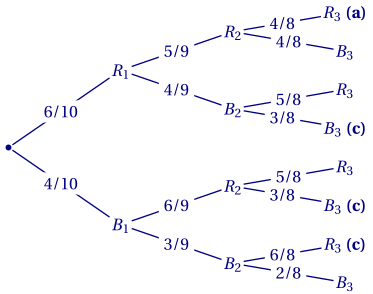
2.a. $P(R_1\cap R_2 \cap R_3) = \dfrac 6 {10} \times \dfrac 5 9 \times \dfrac 4 8 = \dfrac 1 6$.

2.b. =$P(B_1 \cap B_2 \cap B_3) = \dfrac 4 {10} \times \dfrac 3 9 \times \dfrac 2 8 = \dfrac 1 {30}$.

2.c. 3 parcours dans l'arbre correspondent à l'événement «deux boules bleues tirées». \begin{align*} &P(R_1 \cap B_2 \cap B_3) + P(B_1 \cap R_2 \cap B_3) + P(B_1 \cap B_2 \cap R_3)& \\ =&\frac 6 {10} \times \frac 4 {9} \times \frac 3 8 + \frac 4 {10} \times \frac 6 9 \times \frac 3 8 +\frac 4 {10} \times \frac 3 9 \times \frac 6 8& \\ =&3 \times \frac{3\times 4 \times 6}{8\times 9 \times 10}& \\ =&\frac 3 {10}.& \end{align*}

2.c. C'est l'événement contraire de «tirer trois boules bleues». Donc sa probabilité est: \[1 - \frac 1 {30} = \frac{29}{30}.\]

retour