Corrigé du 51 P. 418

retour

1. En notant respectivement $B_i$ et $N_i$ les événements «la $i$-ème boule est blanche/noire», on peut construire l'arbre suivant:

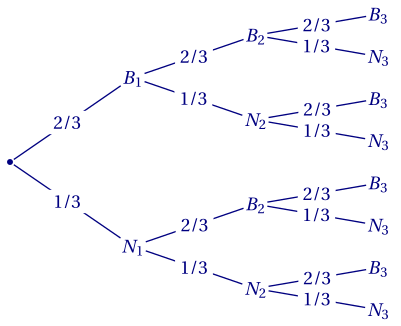
2. Résultats possibles : BBB, BBN, BNB, BNN, NBB, NBN, NNB et NNN.

3.a. Le contraire de cet évènement est «toutes les boules tirées sont de la même couleur», donc sa probabilité est: \begin{align*} P(A) &= 1 - P(B_1\cap B_2 \cap B_3) - P(N_1 \cap N_2 \cap N_3) & \\ &= 1 - \left(\frac 2 3\right)^3 - \left(\frac 1 3\right)^3& \\ &= 1 - \frac 8 {27} - \frac 1 {27}& \\ &= 1 - \frac 1 3& \\ &= \frac 2 3.& \end{align*}

3.b. Il peut donc y avoir aucune boule noire ou une boule noire: \begin{align*} P(B) =&P(B_1\cap B_2\cap B_3) + P(B_1\cap B_2\cap N_3) \\ &+ P(B_1 \cap N_2\cap B_3) + P(N_1 \cap B_2 \cap B_3)& \\ &= \left(\frac 2 3\right)^3 - 3 \times \left(\frac 2 3\right)^2 \times \frac 1 3& \\ &=\frac 8 {27} + \frac{12}{27}& \\ &=\frac{20}{27}.& \end{align*}

3.c. L'événement $A\cap B$ est «on a tiré exactement une boule noire». Donc: \[P(A\cap B) = 3\times\left(\frac 2 3\right)^2 \times \frac 1 3 = \frac 4 9.\] D'autre part: \[P(A)\times P(B) = \frac 2 3 \times \frac{20}{27} = \frac{40}{81}.\] Puisque $P(A\cap B) \neq P(A)\times P(B)$, ces événements ne sont pas indépendants.

retour