Corrigé du 85 P. 423
retour
a.
Le nombre $X_1$ de peluches gagnées suit ici la loi binomiale de paramètres $n = 10$
et $p = \dfrac 1 4$.
Son espérance est donc
\[\operatorname E(X_1) = np = 10\times \frac 1 4 = 2,5.\]
On devrait donc avoir environ 2,5 peluches pour un budget de 10€.
b. Le nombre $X_2$ de peluches gagnées avec 7 euros suit la loi binomiale de paramètres $n=7$ et $p=\dfrac 1 4$. Donc: \[P(X_2=3) = \binom{2}{7} \times \left(\frac14\right)^2 \times \left(\frac34\right)^5 \approx 0,173.\] Le nombre $X_3$ de peluches gagnées avec 5 euros suit la loi binomiale de paramètres $n=5$ et $p=\dfrac 1 4$. Donc: \[P(X_3=0) = \left(\frac 3 4\right)^5 \approx 0,2373.\]
c.
Ici, le nombre $X_4$ de peluches suit la loi binomiale de paramètre $n$ (à déterminer) et $p=\dfrac 1 4$.
On veut avoir:
\[P(X_4 \ge 1) = 1 - P(X_4 = 0) = 1 - \left(1 - \dfrac 1 4\right)^n = 1 - 0,75^n.\]
L'entier $n$ doit donc vérifier
\begin{align*}
1 - 0,75^n &\ge 0,95&
\\ \iff
-0,75^n &\ge -0,05&
\\ \iff
0,75^n &\le 0,05.&
\end{align*}
Méthode 1 : avec logarithme népérien
On a:
\begin{align*}
0,75^n &\le 0,05.&
\\\iff
\ln\left(0,75^n\right) &\le \ln(0,05)&
\\ \iff
n\underbrace{\ln(0,75)}_{\scriptstyle\text{négatif !}}&\le \ln(0,05)&
\\ \iff
n &\ge \frac{\ln(0,05)}{\ln(0,75)}.&
\end{align*}
Puisque $\dfrac{\ln(0,05)}{\ln(0,75)} \approx 10,41$, il faut que $n$ soit au moins égal à 11.
Il faut donc investir 11 euros.
Méthode 2 : par essais successifs On calcule à l'aide de la calculatrice les puissances successives de 0,75.
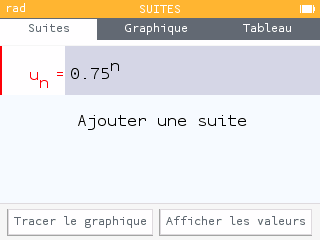
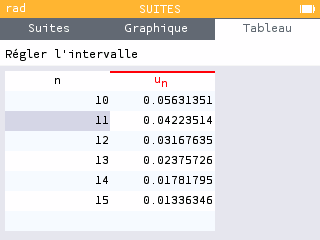
retour