Corrigé du 87 P. 423

retour

Il y a dans l'urne 3 boules rouges et $n$ boules blanches pour un total de $n+3$ boules.

a. Arbre pondéré:

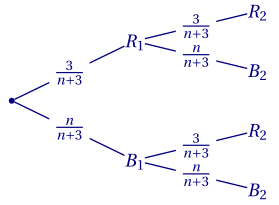
b. Soit $G$ la variable aléatoire donnant le gain du joueur à ce jeu. Sa loi est donc : \[\begin{aligned} P(G=-14) =& P(R_1 \cap R_2) = \left(\frac 3 {n+3}\right)^2 = \frac 9 {(n+3)^2}\;;&\\ P(G=-5) =& P(R_1\cap B_2) + P(B_1 \cap B_2)& \\ =& 2\times \frac 3 {n+3} \times \frac n {n+3} = \frac{3n}{(n+3)^2}\;;&\\ P(G=4) =& P(B_1\cap B_2) = \left(\frac n {n+3}\right)^2 = \frac{n^2}{(n+3)^2}.& \end{aligned}\] Le jeu est financièrement intéressant pour le joueur si l'espérance de $G$ est positive, donc si: \[\begin{aligned} &-14\times \frac 9 {(n+3)^2} - 5\times \frac{3n}{(n+3)^2} + 4\times \frac{n^2}{(n+3)^2} \ge 0&\\ \iff &\frac{-126 -15n + 4n^2}{(n+3)^2} \ge 0&\\ \iff&-126 - 15n + 4n^2 \ge 0.& \end{aligned}\] Étudions le signe du polynôme de degré 2 $4x^2 - 15x - 126$.
Son discriminant est $\Delta = 2241$. Il est positif, donc le polynôme a deux racines \[x_1 = \frac{15-\sqrt{2241}}{8}\approx -4,04\quad\text{et}\quad x_2 = \frac{15+\sqrt{2241}} 8\approx 7,79.\] Le coefficient principal est positif, donc le polynôme est positif sur \[\left]-\infty;\frac{15-\sqrt{2241}} 8\right] \cup \left[\frac{15+\sqrt{2241}} 8;+\infty\right[.\] Sachant que $n$ est un entier positif, il faut donc que $n$ soit au moins égal à 8.

retour