EX-01
retour
On donne ci-dessous la courbe $\mathscr C_f$ d'une fonction $f$ définie sur $]-\infty;-2[\cup]-2;+\infty[$.
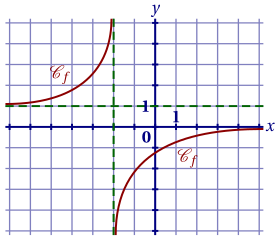
1. Conjecturer, à partir de cette représentation graphique, les limites suivantes: \[\lim_{x\to -\infty} f(x);\quad \lim_{x\to+\infty} f(x);\quad \lim_{\substack{x\to-2\\x < -2}} f(x) \quad\text{et}\quad \lim_{\substack{x\to -2\\x > -2}} f(x).\]
Dans la suite, on considère admises ces conjectures.
2. Donner les équations des asymptotes à $\mathscr C_f$.
3. $g$ est la fonction définie sur $]-\infty;-2[\cup]-2;+\infty[$ par $g(x) = \dfrac 1 {f(x)}$.
a. Donner: \[\lim_{x\to -\infty} g(x);\quad \lim_{x\to +\infty} g(x) \quad\text{et}\quad \lim_{\substack{x\to-2\\x>-2}} g(x).\]
b. La fonction $g$ admet-elle une limite en $-2$? Justifier votre réponse.
Donc la fonction $g$ admet bien une limite en $-2$ car
$\displaystyle\lim_{\substack{x\to-2\\x<-2}} g(x) = \displaystyle\lim_{\substack{x\to-2\\x>-2}} g(x) = \displaystyle\lim_{x\to-2} g(x) = 0$.
retour
code : 1861