retour

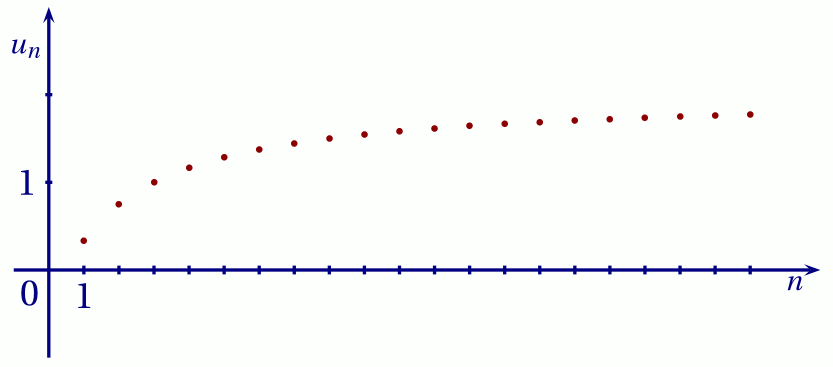
Soit la suite $(u_n)$ définie pour tout entier naturel $n$ par : \[u_n = \frac{2n-1}{n+2}.\] On donne ci-dessous une représentation graphique des premiers termes de cette suite.

1. D'après la représentation graphique, émettre une conjecture concernant un majorant possible de cette suite.
   Corrigé
   Il semble que cette suite soit majorée par 2.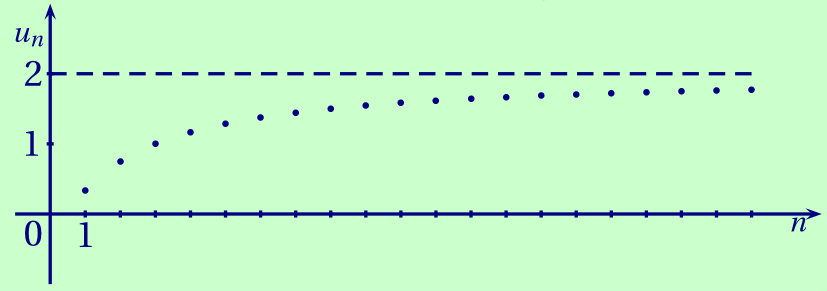

   
2. 1. Montrer que pour tout entier naturel $n$ : \[u_n - 2 = \frac{-5}{n+2}.\] Corrigé
      Pour tout entier naturel $n$ : \[\begin{aligned} u_n - 2 &= \frac{2n-1}{n+2} - 2& \\ &=\frac{2n-1 - 2(n+2)}{n+2}& \\ &=\frac{2n - 1 - 2n - 4}{n+2}& \\ &=\frac{-5}{n+2}.& \end{aligned}\]
   2. En déduire le signe de $u_n - 2$.
      Conclure.
      Corrigé
      Puisque $n\geqslant 0$, alors $n+2 > 0$.
      Par contre $-5$ est négatif, donc le quotient $\dfrac{-5}{n+2}$ est négatif.
      Cela signifie que : \[u_n - 2 \le 0 \implies u_n \le 2.\] La suite $(u_n)$ est bien majorée par 2.

retour

code : 199