retour

Partie 1

Soit $g$ la fonction définie sur $[0;+\infty[$ par \[g(x) = \mathrm{e}^x - x\mathrm{e}^x + 1.\]

1. Déterminer la limite de $g$ en $+\infty$.
   Corrigé
   Pour tout $x\in[0;+\infty[$, \[g(x) = \mathrm e^x(1-x)+1.\] Or le premier facteur, $\mathrm e^x$ tend vers $+\infty$ tandis que le deuxième facteur $1-x$ tend vers $-\infty$. Le produit tend donc vers $-\infty$ : \[\lim_{x\to+\infty} \mathrm e^x(1-x) = -\infty.\]
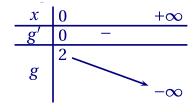
2. Donner le tableau de variations de $g$.
   Corrigé
   $g$ est dérivable sur $[0;+\infty[$ et \[g'(x) = \mathrm e^x - 1\times \mathrm e^x - x\mathrm e^x + 0 = -x\mathrm e^x.\] Une exponentielle étant toujours strictement positive, $g'(x)$ est du signe de $-x$, donc nulle en 0 et strictement négative sur $]0;+\infty[$.
   De plus : \[g(0) = \mathrm e^0 - 0\times \mathrm e^0 + 1 = 1 - 0 +1 = 2.\] On peut donc établir le tableau de variation suivant:
   
3. 1. Démontrer que l'équation $g(x) = 0$ admet sur $[0;+\infty[$ une unique solution.
      On note $\alpha$ cette solution.
      Corrigé
      On remarque que :

      • $g(0) = 2$ et $\displaystyle\lim_{x\to+\infty} g(x) = -\infty$, or $0\in]-\infty;2]$.
      • $g$, dérivable, est donc continue sur $[0;+\infty[$.

      Donc l'équation $g(x)= 0$ admet nécessairement au moins une solution sur $[0;+\infty[$.
      Mais on sait de plus que $g$ est strictement monotone (décroissante) sur $[0;+\infty[$. Donc il y a exactement une solution sur $[0;+\infty[$.
   2. À l'aide de la calculatrice, déterminer un encadrement d'amplitude $10^{-2}$ de $\alpha$.
      Corrigé
      Avec la calculatrice, on obtient que : \[\begin{aligned} g(1,27)&\approx 0,039>0& \\ g(1,28)&\approx -0,007 < 0.& \end{aligned}\] On peut donc dire que $\alpha \in ]1,27\:;\:1,28[$.
   3. Démontrer que \[\mathrm{e}^{\alpha} = \dfrac{1}{\alpha - 1}.\] Corrigé
      Puisque $\alpha$ est l'unique solution de $g(\alpha) = 0$, on a : \[\begin{aligned} \mathrm e^{\alpha} - \alpha\mathrm e^{\alpha} + 1 &=0& \\ \iff \mathrm e^{\alpha} - \alpha\mathrm e^{\alpha} &=-1& \\ \iff \mathrm e^{\alpha}(1-\alpha) &= -1& \\ \iff \mathrm e^{\alpha} &= -\frac 1 {1 - \alpha}& \\ \iff \mathrm e^{\alpha} &= \frac 1 {\alpha - 1}.& \end{aligned}\]
4. Déterminer le signe de $g(x)$ suivant les valeurs de $x$.
   Corrigé
   $g$ est strictement décroissante sur $[0;+\infty[$ et s'annule en $\alpha$.
   Elle est donc strictement positive sur $[0;\alpha[$, nulle en $\alpha$ et strictement négative sur $]\alpha;+\infty[$.

Partie 2

Soit $A$ la fonction définie et dérivable sur $[0;+\infty[$ telle que \[A(x) = \dfrac{4x}{\mathrm{e}^x + 1}.\]

1. Démontrer que pour tout réel $x$ positif ou nul, $A'(x)$ a le même signe que $g(x)$, où $g$ est la fonction définie dans la partie 1.
   Corrigé
   Pour tout $x\in[0;+\infty[$: \[\begin{aligned} A'(x) &= \frac{4\left(\mathrm e^x + 1\right) - 4x\left(\mathrm e^x\right)}{\left(\mathrm e^x + 1\right)^2}& \\ &=\frac{4\left[\mathrm e^x + 1 - x\mathrm e^x\right]}{\left(\mathrm e^x + 1\right)^2}& \\ &=\frac{4g(x)}{\left(\mathrm e^x+1\right)^2}.& \end{aligned}\] Or $\left(\mathrm e^x + 1\right)^2$ et 4 sont positifs, donc $A'(x)$ est du signe de $g(x)$ (étudié précédemment).
2. En déduire les variations de la fonction $A$ sur $[0;+\infty[$.
   Corrigé
   On en conclut que $A$ est croissante sur $[0;\alpha]$ et décroissante sur $[\alpha;+\infty[$.

Partie 3

On considère la fonction $f$ définie sur $[0;+\infty[$ par \[f(x) = \dfrac{4}{\mathrm{e}^x + 1}.\] On note $(\mathcal{C})$ sa courbe représentative dans un repère orthonormé $(O;\vec i,\vec j)$.

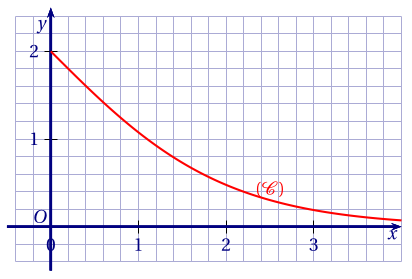
Pour tout réel $x$ positif ou nul, on note :

• $M$ le point de $(\mathcal{C})$ de coordonnées $(x;f(x))$,
• $P$ le point de coordonnées $(x;0)$,
• $Q$ le point de coordonnées $(0;f(x))$.

1. Démontrer que l'aire du rectangle $OPMQ$ est maximale lorsque $M$ a pour abscisse $\alpha$.
   On rappelle que le réel $\alpha$ a été défini dans la partie 1.
   Corrigé
   L'aire du rectangle $OPMQ$ se calcule par : \[OP\times PM = x f(x) = x\times \frac 4 {\mathrm e^x + 1} = \frac {4x}{\mathrm e^x +1} = A(x).\] (On sait donc dorénavant pourquoi cette fonction s'appelait $A$!)
   Or on a vu que $A$ est croissante sur $[0;\alpha]$ puis décroissante sur $[\alpha;+\infty[$. Elle admet donc un maximum unique en $\alpha$.
2. Le point $M$ a pour abscisse $\alpha$.
   La tangente $(T)$ en $M$ à la courbe $(\mathcal{C})$ est-elle parallèle à la droite $(PQ)$ ?
   Corrigé
   Pour étudier le parallélisme de ces droites, on va déterminer leurs coefficients directeurs.
   $f$ est dérivable sur $[0;+\infty[$ et : \[f'(x) = \frac{-4\mathrm e^x}{\left(\mathrm e^x + 1\right)^2}.\] Le coefficient directeur de la tangente est : \[f'(\alpha) = \frac{-4\mathrm e^{\alpha}}{\left(\mathrm e^{\alpha} + 1\right)^2}.\] Or on a vu précédemment que : \[\mathrm e^{\alpha} = \dfrac 1 {\alpha - 1},\] donc \[\begin{aligned} f'(\alpha) &=\frac{-4\mathrm e^{\alpha}}{\left(\mathrm e^{\alpha} + 1\right)^2} =\frac{-4\times \frac 1 {\alpha - 1}}{\left(\frac 1 {\alpha - 1} + 1\right)^2}& \\ &=\frac{-\frac 4 {\alpha - 1}}{\left(\frac{\alpha}{\alpha - 1}\right)^2} =-\frac 4 {\alpha - 1} \times \frac{\left(\alpha - 1\right)^2}{\alpha^2}& \\ &=-\frac{4(\alpha - 1)}{\alpha^2}.& \end{aligned}\] Le coefficient directeur de $(PQ)$ est : \[\begin{aligned} \frac{y_Q - y_P}{x_Q - x_P} &=\frac{\frac 4 {\mathrm e^x + 1} - 0}{0 - \alpha} =\frac{-4}{\alpha(\mathrm e^{\alpha} + 1)}& \\ &=\frac{-4}{\alpha\left(\frac 1 {\alpha -1} + 1\right)} =\frac{-4}{\alpha \times \frac{\alpha}{\alpha - 1}}& \\ &=\frac{-4}{\frac{\alpha^2}{\alpha - 1}} =-\frac{4(\alpha -1)}{\alpha^2}.& \end{aligned}\] Puisque la tangente et la droite $(PQ)$ ont le même coefficient directeur, elles sont parallèles.

retour

code : 239