EX-25

retour

Partie 1.

On rappelle les résultats suivants concernant le produit scalaire de deux vecteurs.
Soient, dans un repère orthonormé, deux vecteurs $\vec u(x,y)$ et $\vec v(x',y')$.

On appelle produit scalaire de ces deux vecteurs le nombre réel: \[\vec u \cdot \vec v = xx' + yy'.\]
Les vecteurs $\vec u$ et $\vec v$ sont orthogonaux si et seulement si $\vec u\cdot \vec v = 0$.

Soient $D$ une droite de coefficient directeur $m$ non nul et $D'$ une droite de coefficient directeur $m'$ non nul.\par
En utilisant le préambule, démontrer que $D$ et $D'$ sont perpendiculaires si et seulement si \[mm'=-1.\]

Corrigé

Puisque $m$ est le coefficient directeur de $D$, le vecteur $\vec u(1;m)$ est un vecteur directeur de $D$. De même, le vecteur $\vec u'(1;m')$ est un vecteur directeur de $D'$.
Les droites $D$ et $D'$ sont perpendiculaires si et seulement si les vecteurs $\vec u$ et $\vec u'$ sont orthogonaux, ce qui se traduit encore par \begin{align*} \vec u \cdot \vec u' &= 0&\\ \iff 1\times 1 + m\times m' &=0&\\ \iff mm' &= -1 & \end{align*}

Partie 2.

Soient $f$ et $g$ les fonctions définies sur l'ensemble $\mathbb R$ des nombres réels par \[f(x) = \mathrm{e}^x\qquad \text{et}\qquad g(x) = \mathrm{e}^{- x}.\] On note $\mathcal{C}_f$ la courbe représentative de la fonction $f$ et $\mathcal{C}_g$ celle de la fonction $g$ dans un repère orthonormé du plan.

Pour tout réel $a$, on note $M$ le point de $\mathcal{C}_f$ d'abscisse $a$ et $N$ le point de $\mathcal{C}_g$ d'abscisse $a$.

La tangente en $M$ à $\mathcal{C}_f$ coupe l'axe des abscisses en $P$, la tangente en $N$ à $\mathcal{C}_g$ coupe l'axe des abscisses en $Q$.

À l'aide d'un logiciel de géométrie dynamique, on a représenté la situation pour différentes valeurs de $a$.

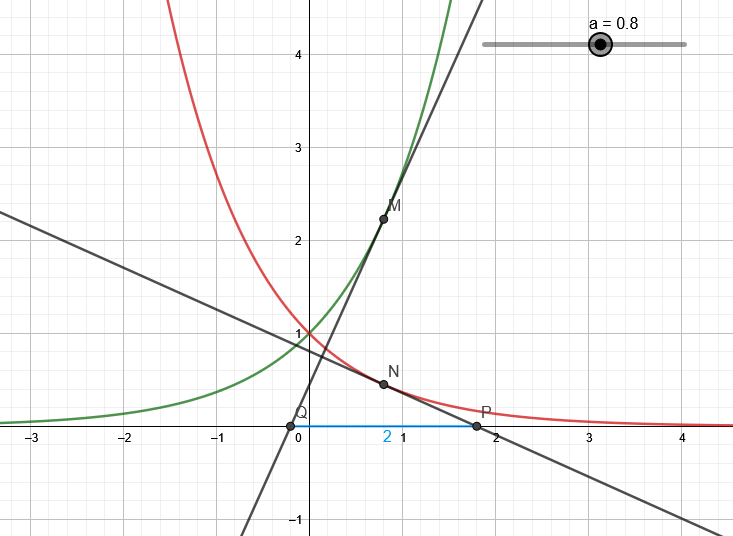
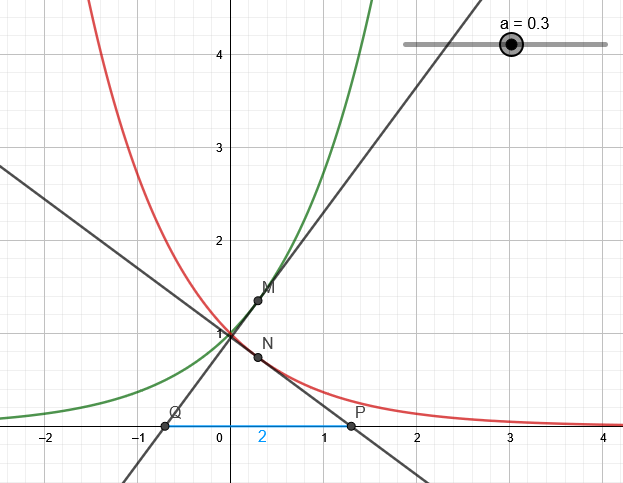
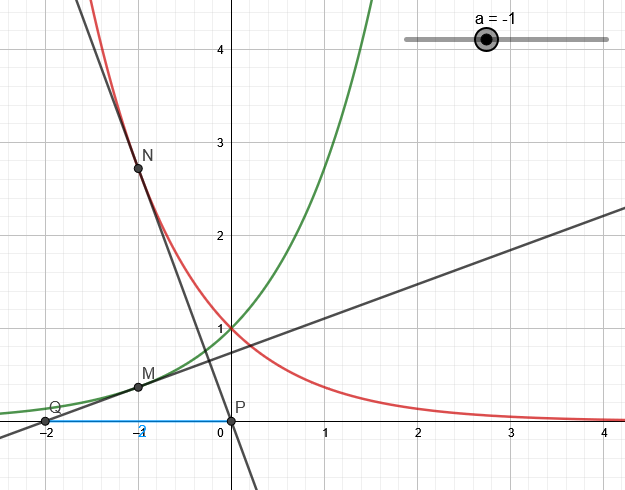
1. Démontrer que la tangente en $M$ à $\mathcal{C}_f$ est perpendiculaire à la tangente en $N$ à $\mathcal{C}_g$.

Corrigé

Pour tout réel $x$ on a: \[f'(x) = \mathrm e^x \qquad\text{et}\qquad g'(x) = \mathrm -e^{-x}\] La tangente à $\mathscr C_f$ au point d'abscisse $a$ admet pour coefficient directeur $f'(a) =\mathrm e^a$ et la tangente à $\mathscr C_g$ au point d'abscisse $a$ admet pour coefficient directeur $g'(a) = -\mathrm e^{-a}$.
Or: \[\mathrm e^{a} \times \left(-\mathrm e^{-a}\right) = -\mathrm e^{a-a} = -\mathrm e^0 = -1.\] Donc selon la partie 1, ces tangentes sont bien perpendiculaires.

2. Démontrer que, quelle que soit la valeur de $a$, $PQ=2$.

Corrigé

L'équation de la tangente à $\mathscr C_f$ est: \begin{align*} y &= f'(a)(x-a) + f(a)&\\ \iff y&= \mathrm e^a(x-a) + \mathrm e^a&\\ \iff y &= \mathrm e^a(x-a+1)& \end{align*} Le point $P$ est le point de cette tangente d'ordonnée nulle et son abscisse est donc: \[\mathrm 0=e^a(x-a+1) \iff 0=x -a +1 \iff x = a - 1.\] $P$ a donc pour coordonnées $(a-1;0)$.
L'équation de la tangente à $\mathscr C_g$ est: \begin{align*} y&=g'(a)(x-a) + g(a)&\\ y&=-\mathrm e^{-a}(x - a) + \mathrm e^{-a}&\\ \iff y&=\mathrm e^{-a}(-x+a+1)& \end{align*} Le point $Q$ est le point d'ordonnée nulle de cette droite et son abscisse est donc: \[0 = \mathrm e^{-a}(-x+a+1) \iff 0 = -x+a + 1 \iff x = a + 1.\] $Q$ a donc pour coordonnées $(a+1;0)$.
La distance $PQ$ est donc: \[\begin{aligned} PQ &= \sqrt{(x_Q - x_P)^2 + (y_Q - y_P)^2}& \\ &= \sqrt{(1-1)^2 + (a+1-a+1)^2}& \\ &=\sqrt{2^2}=2.& \end{aligned}\]

retour

code : 2585