EX-23

retour

Partie A

Voici deux courbes $\mathcal{C}_1$ et $\mathcal{C}_2$ qui donnent pour deux personnes $P_1$ et $P_2$ de corpulences différentes la concentration $C$ d'alcool dans le sang (taux d'alcoolémie) en fonction du temps $t$ après ingestion de la même quantité d'alcool.

L'instant $t = 0$ correspond au moment où les deux individus ingèrent l'alcool.

$C$ est exprimée en gramme par litre et $t$ en heure.

Définition : La corpulence est le nom scientifique correspondant au volume du corps

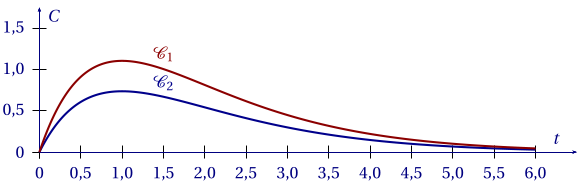
1. La fonction $C$ est définie sur l'intervalle $[0;+\infty[$ et on note $C'$ sa fonction dérivée. À un instant $t$ positif ou nul, la vitesse d'apparition d'alcool dans le sang est donnée par $C'(t)$.
À quel instant cette vitesse est-elle maximale?

Corrigé

C'est à l'instant $t=0$ que la vitesse d'absorption est la plus rapide, car c'est l'abscisse du point de la courbe ($\mathcal C_1$ ou $\mathcal C_2$) où la tangente a la pente la plus forte.

2. Sur le graphique précédent, identifier la courbe correspondant à la personne la plus corpulente. Justifier le choix effectué.

Corrigé

Plus la personne est corpulente, plus la même quantité d'alcool sera diluée, donc la courbe représentant la personne la plus corpulente est celle dont le maximum est le moins élevé. C'est donc la courbe $\mathcal C_2$.

3. Une personne à jeun absorbe de l'alcool. On admet que la concentration $C$ d'alcool dans son sang peut être modélisée par la fonction $f$ définie sur $[0;+\infty[$ par \[f(t) = At\mathrm{e}^{-t}\] où $A$ est une constante positive qui dépend de la corpulence et de la quantité d'alcool absorbée.

a. On note $f'$ la fonction dérivée de la fonction $f$. Déterminer $f'(0)$.

Corrigé

Pour tout réel positif $t$. \[f'(t) = A\mathrm e^{-t} + At\left(-\mathrm e^{-t}\right) = A\mathrm e^{-t}-At\mathrm e^{-t} =A\mathrm e^{-t}(1- t).\] Donc $f'(0) = A\mathrm e^0(1-0) = A$.

b. On dit souvent qu'une personne de faible corpulence subit plus vite les effets de l'alcool.
L'affirmation suivante est-elle vraie?
« À quantité d'alcool absorbée égale, plus $A$ est grand, plus la personne est corpulente. ».

Corrigé

Faux. Car plus $A$ est grand, plus $f'(0)$ est grand, donc plus la vitesse d'absorption est rapide, donc moins la personne est corpulente.

Partie B - Un cas particulier

Paul, étudiant de 19 ans de corpulence moyenne et jeune conducteur, boit deux verres de rhum. La concentration $C$ d'alcool dans son sang est modélisée en fonction du temps $t$, exprimé en heure, par la fonction $f$ définie sur $[0;+\infty[$ par \[f(t) = 2t\mathrm{e}^{-t}.\]

1. Étudier les variations de la fonction $f$ sur l'intervalle $[0;+\infty[$.

Corrigé

La fonction $f$ est dérivable sur $[0;+\infty[$ et pour tout $t\in[0;+\infty[$: \[f'(t)= 2\mathrm e^{-t}+2t\left(-\mathrm e^{-t}\right)=2\mathrm e^{-t}-2t\mathrm e^{-t} =2\mathrm e^{-t}(1-t).\] Puisque $2>0$ et $\mathrm e^{-t}>0$ pour tout réel $t$, $f'(t)$ est du signe de $(1-t)$. Donc

Pour tout $t\in [0;1[$, $f'(t)>0$ donc $f$ est strictement croissante sur $[0;1]$.
Pour tout $t\in]1:+\infty[$, $f'(t)<0$ donc $f$ est strictement décroissante sur $[1;+\infty[$.

2. À quel instant la concentration d'alcool dans le sang de Paul est-elle maximale? Quelle est alors sa valeur? Arrondir à 10⁻² près.

Corrigé

D'après ses variations, $f$ admet son maximum en $t=1$. Ce maximum est donné par \[f(1)= 2\times 1 \times \mathrm e^{-1} = \frac 2 {\mathrm e} \approx 0,74.\] La concentration maximale d'alcool dans le sang de Paul avoisinera donc 0,74 g.L^-1.

3. Rappeler la limite de $\dfrac{\mathrm{e}^t}{t}$ lorsque $t$ tend vers $+\infty$ et en déduire celle de $f(t)$ en $+ \infty$.
Interpréter le résultat dans le contexte de l'exercice.

Corrigé

On sait que $\displaystyle\lim_{t\to+\infty}\dfrac{\mathrm e^t}t = +\infty$, donc que $\displaystyle\lim_{t\to+\infty}\dfrac t{\mathrm e^t} = 0$.
Or \[f(t) = 2t\mathrm e^{-t} = 2\times \frac{t}{\mathrm e^t} \implies \lim_{t\to+\infty} f(t) = 2\times 0 = 0.\] Bonne nouvelle, Paul finira par éliminer tout l'alcool absorbé (enfin, s'il ne consomme pas à nouveau de l'alcool bien sûr !).

4. Paul veut savoir au bout de combien de temps il peut prendre sa voiture. On rappelle que la législation autorise une concentration maximale d'alcool dans le sang de 0,2 g.L^-1 pour un jeune conducteur.

a. Démontrer qu'il existe deux nombres réels $t_1$ et $t_2$ tels que $f\left(t_1\right) = f\left(t_2\right) = 0,2$.

Corrigé

La fonction $f$ est continue, strictement croissante et $f(0)<0,2$ tandis que $f(1)>0,2$.
L'équation $f(x)= 0,2$ admet donc une unique solution $t_1$ dans $]0;1[$.
De même, $f$ est continue, strictement décroissante et $f(1)>0,2$ tandis que $\displaystyle\lim_{t\to+\infty} f(t) = 0<0,2$.
L'équation $f(t)=0,2$ admet donc une unique solution $t_2$ dans l'intervalle $]1;+\infty[$.
Il existe donc bien exactement deux réels $t_1$ et $t_2$ tels que $f(t_1)=f(t_2)=0,2$.

b. Quelle durée minimale Paul doit-il attendre avant de pouvoir prendre le volant en toute légalité?
Donner le résultat arrondi à la minute la plus proche.

Corrigé

Paul doit donc attendre jusqu'à $t_2$. Une recherche à la calculatrice montre que: \[\begin{aligned} & \begin{cases} f(3,577)\approx 0,20002\\f(3,578)\approx 0,19988 \end{cases} & \\ \implies & 3,577 < t_2 < 3,578 & \\ \implies &t_2 \approx 3,58.& \end{aligned}\] Paul doit donc attendre au moins 60×3,58≈215 minutes, soit 3 heures et 35 minutes.

5. La concentration minimale d'alcool détectable dans le sang est estimée à 5×10^-3 g.L^-1.

a. Justifier qu'il existe un instant $T$ à partir duquel la concentration d'alcool dans le sang n'est plus détectable.

Corrigé

Puisque $\displaystyle\lim_{t\to+\infty} f(t) = 0$, il existe un réel $T$ tel que \[t > T \implies f(t) < 5\times 10^{-3}.\]

b. On donne ci-dessous un programme Python

Déterminer la valeur affichée par ce programme.
Que représente cette valeur?

Corrigé

L'algorithme renvoie la valeur $8,25$.
Elle représente, au quart d'heure près, le temps nécessaire pour que l'alcool présent dans le sang de Paul devienne indétectable.

retour

code : 2837