EX-08
retour
On considère les fonctions dérivables sur $\mathbb R$ \[f:\ x\mapsto -\mathrm e^{-12x}\quad\text{et}\quad g:\ x\mapsto 4\mathrm e^{3x}- 5.\] On a représenté ces deux fonctions à l'aide d'une calculatrice graphique.
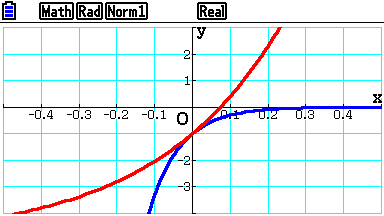
1. Conjecturer les coordonnées d'un point en lequel elles admettent une tangente commune.
Corrigé
Les deux courbes semblent admettre une tangente commune au point de coordonnées $(0;-1)$.
2. Valider ou invalider cette conjecture par le calcul.
Corrigé
$f(0) = \mathrm e^{-12\times 0} = 1$ et $g(0) = 4\mathrm e^{3\times 0} - 5 = 4\times 1 - 5 = -1$.
Les deux courbes passent par le point de coordonnées $(0;-1)$. Donc les tangentes au point d'abscisse 0 des deux courbes passent aussi par ce point.
$f$ est dérivable en tout $x\in\mathbb R$ et \[f'(x) = -(-12\mathrm e^{-12x} = 12\mathrm e^{-12x}.\] Donc: $f'(0) = 12\mathrm e^{-12\times 0} = 12\times 1 = 12$.
De même, $g$ est dérivable en tout $x\in\mathbb R$ et \[g'(x) = 4(3\mathrm e^{3x}) - 0 = 12\mathrm e^{3x}.\] Donc : $g'(0) = 12\mathrm e^{3\times 0} = 12$. Les tangentes au point d'abscisse 0 admettent donc le même coefficient directeur; elles sont donc parallèles. Mais elles passent aussi par un même point, donc elles sont confondues.
Notre conjecture est donc validée.
Les deux courbes passent par le point de coordonnées $(0;-1)$. Donc les tangentes au point d'abscisse 0 des deux courbes passent aussi par ce point.
$f$ est dérivable en tout $x\in\mathbb R$ et \[f'(x) = -(-12\mathrm e^{-12x} = 12\mathrm e^{-12x}.\] Donc: $f'(0) = 12\mathrm e^{-12\times 0} = 12\times 1 = 12$.
De même, $g$ est dérivable en tout $x\in\mathbb R$ et \[g'(x) = 4(3\mathrm e^{3x}) - 0 = 12\mathrm e^{3x}.\] Donc : $g'(0) = 12\mathrm e^{3\times 0} = 12$. Les tangentes au point d'abscisse 0 admettent donc le même coefficient directeur; elles sont donc parallèles. Mais elles passent aussi par un même point, donc elles sont confondues.
Notre conjecture est donc validée.
retour
code : 2846