retour

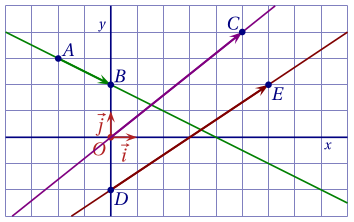
On considère la figure ci-dessous.

1. 1. Par lecture graphique, préciser les coordonnées du vecteur $\overrightarrow{AB}$.
      Corrigé
      Les vecteurs $\vec i$ et $\vec j$ ont pour norme un carreau. On va de $A$ en $B$ en se déplaçant de 2 carreaux dans le sens de $\vec i$ et de 1 carreau dans le sens de $-\vec j$.
      On lit donc : $\overrightarrow{AB}\begin{pmatrix}2\\-1\end{pmatrix}$.
   2. En déduire le coefficient directeur de la droite $(AB)$.
      Corrigé
      $\overrightarrow{AB}$ est un vecteur directeur de la droite $(AB)$ donc son coefficient directeur est \[\frac{-1}{2} = -\frac 1 2.\]
2. Mêmes questions pour le vecteur $\overrightarrow{OC}$ et la droite $(OC)$.
   Corrigé
   On lit: $\overrightarrow{OC}\begin{pmatrix}5\\4\end{pmatrix}$.
   Donc le coefficient directeur de la droite $(OC)$ est $\dfrac 4 5$.
3. Mêmes question pour le vecteur $\overrightarrow{DE}$ et la droite $(DE).$
   Corrigé
   On lit : $\overrightarrow{DE}\begin{pmatrix}6\\4\end{pmatrix}$.
   Donc le coefficient directeur de $(DE)$ est \[\dfrac 4 6 = \dfrac 2 3.\]

retour

code : 352