EX-14

retour

$f$, $g$ et $h$ sont trois fonctions dont on donne ci-dessous les tableaux de variations.

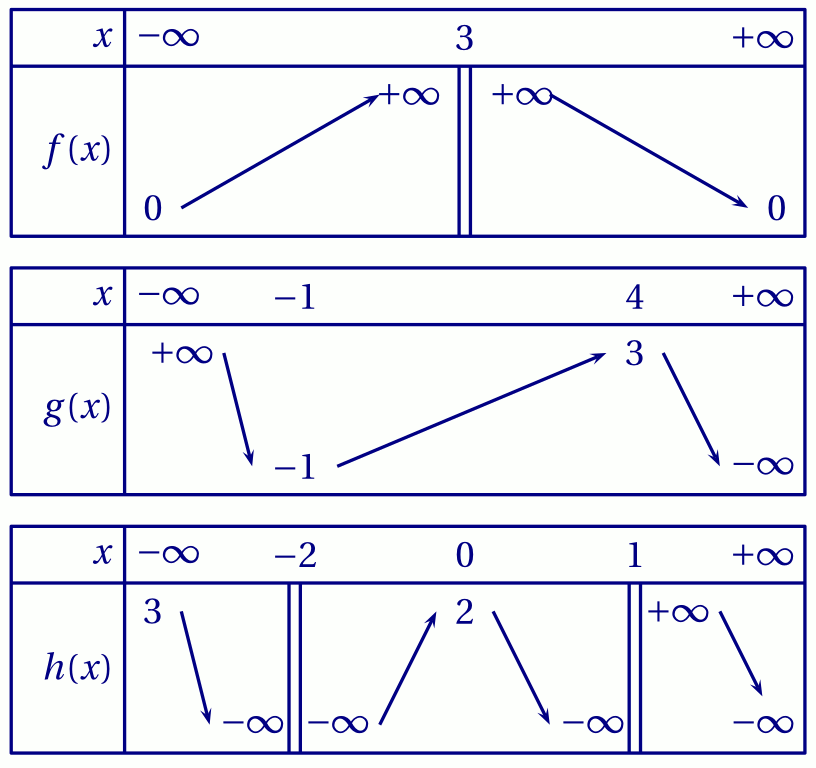
Pour chacune de ces fonctions :

a. Préciser sur quel(s) intervalle(s) elle est continue ;
Corr. pour f Corr. pour g Corr. pour h

$f$ est continue sur $]-\infty;3[$ et sur $]3;+\infty[$.

$g$ est continue sur $\mathbb R$.

$h$ est continue sur $]-\infty;-2[$, $]-2;1[$ et $]1;+\infty[$.

b. Donner les limites aux bornes de son ensemble de définition ;
Corr. pour f Corr. pour g Corr. pour h

$\displaystyle\lim_{x\to-\infty} f(x) = 0$, $\displaystyle\lim_{x\to 3} f(x) = +\infty$ et $\displaystyle\lim_{x\to+\infty} f(x) = 0$.

$\displaystyle\lim_{x\to-\infty} g(x) = +\infty$ et $\displaystyle\lim_{x\to+\infty} g(x) = -\infty$.

$\displaystyle\lim_{x\to-\infty} h(x) = 3$, $\displaystyle\lim_{x\to-2} h(x)=-\infty$, $\displaystyle\lim_{x\to 1^{-}} h(x)=-\infty$, $\displaystyle\lim_{x\to 1^+} h(x)=+\infty$ et $\displaystyle\lim_{x\to+\infty} h(x) = -\infty$.

c. Donner les équations des éventuelles asymptotes horizontales ou verticales à sa courbe.
Corr. pour f Corr. pour g Corr. pour h

$\mathscr C_f$ admet la droite d'équation $y = 0$ comme asymptote horizontale et la droite d'équation $x=3$ comme asymptote verticale.

$\mathscr C_g$ n'admet ni asymptote horizontale, ni asymptote verticale.

$\mathscr C_h$ admet la droite d'équation $y=3$ pour asymptote horizontale et les droites d'équations $x=-2$ et $x=1$ pour asymptotes verticales.

retour

code : 414