EX-15
retour
Soit $f$ la fonction définie sur $\mathbb R$ par \[f(x)=\begin{cases} 3+x\ \text{si}\ x\le -1 \\ x^2+x\ \text{si}\ x>-1 \end{cases} \]
1.
Représenter graphiquement la fonction $f$.
Corrigé
Sur $]-\infty;-1]$, $f$ est assimilable à une fonction affine,
donc représentée par une demi-droite de coefficient directeur $1$
et qui, prolongée, passerait pas le point de coordonnées $(0;3)$.
Sur $]-1;+\infty[$, $f$ est assimilable à une fonction polynôme, donc représentée par un arc de parabole.
Le sommet de cette parabole admet pour coordonnées : \[\begin{aligned} x &= -\frac b{2a} = -\frac 1 2\;;& \\ y &= f\left(-\frac 1 2\right) = \left(-\frac 1 2\right)^2 -\frac 1 2 = \frac 1 4 - \frac 1 2 = -\frac 1 4.& \end{aligned}\] De plus \[\begin{aligned} f(1) &= 1^2 + 1= 2& \\ f(2) &=2^2+2=4+2 = 6.& \end{aligned}\] On obtient donc la figure ci-dessous.
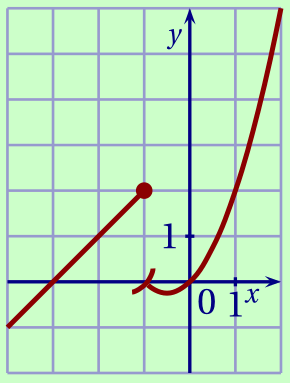
Sur $]-1;+\infty[$, $f$ est assimilable à une fonction polynôme, donc représentée par un arc de parabole.
Le sommet de cette parabole admet pour coordonnées : \[\begin{aligned} x &= -\frac b{2a} = -\frac 1 2\;;& \\ y &= f\left(-\frac 1 2\right) = \left(-\frac 1 2\right)^2 -\frac 1 2 = \frac 1 4 - \frac 1 2 = -\frac 1 4.& \end{aligned}\] De plus \[\begin{aligned} f(1) &= 1^2 + 1= 2& \\ f(2) &=2^2+2=4+2 = 6.& \end{aligned}\] On obtient donc la figure ci-dessous.

2.
$f$ est-elle continue sur $\mathbb R$?
Corrigé
Sur $]-\infty;-1]$, $f$ est une fonction affine donc continue.
De même, sur $]-1;+\infty[$, $f$ est une fonction polynôme donc aussi continue.
Par contre, en −1 : \[ \lim_{x\to-1^+} f(x)=\lim_{x\to -1^+} x^2 + x = (-1)^2 + (-1) = 1-1 = 0. \] Puisque \[\lim_{x\to1^+} f(x) \neq f(1)\] il y a une discontinuité au point d'abscisse $-1$.
Donc $f$ n'est pas continue sur $\mathbb R$.
De même, sur $]-1;+\infty[$, $f$ est une fonction polynôme donc aussi continue.
Par contre, en −1 : \[ \lim_{x\to-1^+} f(x)=\lim_{x\to -1^+} x^2 + x = (-1)^2 + (-1) = 1-1 = 0. \] Puisque \[\lim_{x\to1^+} f(x) \neq f(1)\] il y a une discontinuité au point d'abscisse $-1$.
Donc $f$ n'est pas continue sur $\mathbb R$.
retour
code : 415