EX-16
retour
$f$ est la fonction définie sur $\mathbb R$ par: \[\left\{\begin{array}{ll}f(x)=x^2-3x - 2&\ \text{si}\ x\leqslant 1\\ f(x) = \dfrac{x-3} x&\ \text{si}\ x>1 \end{array}\right.\] La fonction $f$ est-elle continue sur $\mathbb R$?
Corrigé
La fonction $x\mapsto x^2 - 3x - 2$ est continue sur $\mathbb R$, donc a fortiori sur $]-\infty;1]$.
La fonction $x\mapsto \dfrac{x-3} x$ est continue sur $]0;+\infty[$, donc a fortiori sur $]1;+\infty[$.
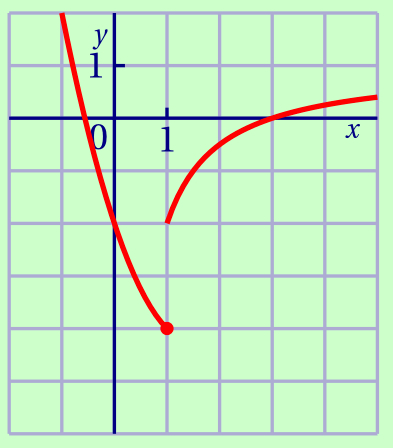
Le seul point de discontinuité possible est donc en 1. Or \[f(1) = 1^2 - 3\times 1 - 2 = -4.\] et \[\lim_{x\to 1^+} f(x) = \lim_{x\to 1^+}\frac{x-3}x = \frac{1-3}{1} =-2.\] Puisque \[\lim_{x\to 1^+} f(x) \neq f(1)\] la fonction $f$ n'est pas continue en 1.
La discontinuité est bien évidente si l'on trace la représentation graphique de cette fonction.
La fonction $x\mapsto \dfrac{x-3} x$ est continue sur $]0;+\infty[$, donc a fortiori sur $]1;+\infty[$.
Le seul point de discontinuité possible est donc en 1. Or \[f(1) = 1^2 - 3\times 1 - 2 = -4.\] et \[\lim_{x\to 1^+} f(x) = \lim_{x\to 1^+}\frac{x-3}x = \frac{1-3}{1} =-2.\] Puisque \[\lim_{x\to 1^+} f(x) \neq f(1)\] la fonction $f$ n'est pas continue en 1.
La discontinuité est bien évidente si l'on trace la représentation graphique de cette fonction.

retour
code : 416