EX-20
retour
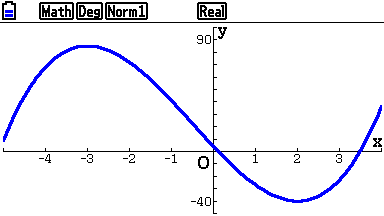
Étudier les variations de la fonction $f$ définie sur $\mathbb R$ par \[f(x) = 2x^3 + 3x^2 - 36x + 4.\]
Corrigé
La fonction $f$ est dérivable sur $\mathbb R$ et pour tout réel $x$ :
\begin{align*}
f'(x) &= 2\times (3x^2) + 3\times (2x) - 36\times 1 + 0&
\\
&=6x^2 + 6x - 36&
\\
&=6(x^2 + x - 6).&
\end{align*}
$f'(x)$ est du signe du polynôme $x^2 + x - 6$.
Son discriminant vaut : \[\Delta = 1^2 - 4\times 1 \times (-6) = 25.\] Il est strictement positif, donc ce polynôme admet deux racines \[x_1 = \frac{-1 -\sqrt{25}} 2= -3 \quad\text{et}\quad x_2 = \frac{-1+\sqrt{25}}2 = 2.\] Son coefficient principal est $1$, positif, donc ce polynôme est positif à l'extérieur de ses racines.
Donc :
Son discriminant vaut : \[\Delta = 1^2 - 4\times 1 \times (-6) = 25.\] Il est strictement positif, donc ce polynôme admet deux racines \[x_1 = \frac{-1 -\sqrt{25}} 2= -3 \quad\text{et}\quad x_2 = \frac{-1+\sqrt{25}}2 = 2.\] Son coefficient principal est $1$, positif, donc ce polynôme est positif à l'extérieur de ses racines.
Donc :
- Sur $]-\infty;-3]$, $f'$ est positive et donc $f$ est croissante.
- Sur $[-3;2]$, $f'$ est négative et donc $f$ est décroissante.
- Sur $[2;+\infty[$, $f'$ est positive et donc $f$ est croissante.

retour
code : 44