EX-21
retour
Dresser le tableau de variations de la fonction $f$ définie sur $\mathbb R$ par \[f(x) = x^3 - 3x^2 - 9x + 1.\] On admettra que \[\lim_{x\to-\infty} f(x) = -\infty \quad\text{et}\quad \lim_{x\to+\infty} f(x) = +\infty.\]
Corrigé
La fonction polynôme $f$ est dérivable sur $\mathbb R$ et pour tout réel $x$ :
\[f'(x) = 3x^2 - 3\cdot 2x - 9 = 3x^2 -6x - 9 = 3(x^2 -2x - 3).\]
$f'(x)$ admet deux racines évidentes, $-1$ et $3$.
C'est un polynôme de degré 2, il n'a donc pas d'autre racine, et puisque son coefficient principal est positif, il est positif à l'extérieur de ses racines.
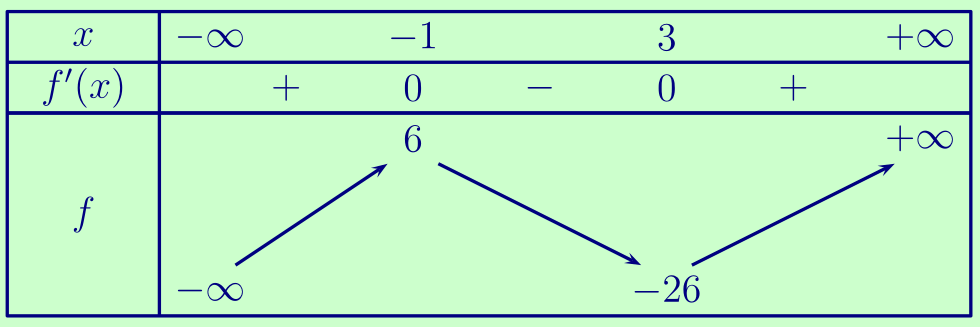Avec
\[\begin{aligned}
f(-1) &= (-1)^3 - 3\times (-1) - 9\times (-1) + 1= 6&
\\
f(3) &= 3^3 - 3\times 3^2 - 9\times 3 + 1 = -26&
\end{aligned}\]
C'est un polynôme de degré 2, il n'a donc pas d'autre racine, et puisque son coefficient principal est positif, il est positif à l'extérieur de ses racines.
retour
code : 45