EX-25

retour

1. On considère la fonction : \[g\ :\ x\mapsto (x-2)\mathrm e^{-2x+6} + 3,\] définie et dérivable sur $\mathbb R$.

1.a. Déterminer une expression de la dérivée de $g$.
Corrigé

Pour tout réel $x$ : \begin{align*} g'(x) &= 1\mathrm e^{-2x+6} + (x-2)\left(-2\mathrm e^{-2x+6}\right) + 0& \\ &=\left[1 - 2(x-2)\right]\mathrm e^{-2x+6}& \\ &=\left[1 - 2x + 4\right]\mathrm e^{-2x+6}& \\ &=(-2x+5)\mathrm e^{-2x+6}.& \end{align*}

b. Donner le tableau de signes de cette dérivée sur $\mathbb R$.
Corrigé

Puisque, pour tout réel $x$, $\mathrm e^{-2x+6}$ est strictement positive, $g'(x)$ est du signe de $(-2x + 5)$.
Or \[-2x + 5 = 0 \iff -2x = -5 \iff x = \frac{-5}{-2} = \frac 5 2.\] et le coefficient directeur est $-2$, négatif ; donc $g'$ est négative à droite de son zéro.

c. En déduire le tableau de variation de $g$ sur $\mathbb R$.
Corrigé

On en déduit les variations de la fonction $g$ :

Avec ici : \[g\left(\frac 5 2\right) =\left(\frac 5 2 - 2\right)\mathrm e^{-2\times \frac 5 2 + 6} + 3 =\frac 1 2 \mathrm e^1 + 3 =\frac 1 2 \mathrm e + 3.\]

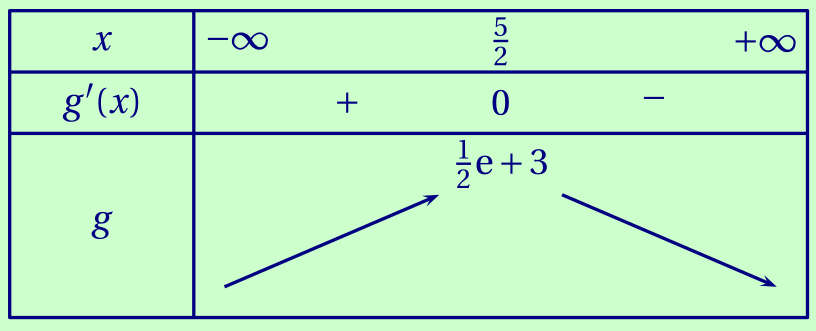
d. On a établi, à l'aide d'une calculatrice, la table de valeurs de la fonction $g$ ci-dessous (en trois écrans).
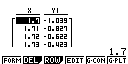
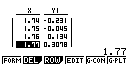
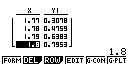
copie écran calculatrice

En déduire un arrondi à 10⁻¹ de l'unique solution de l'équation \[g(x)=0.\] Corrigé

On remarque que $g(1,75) < 0$ tandis que $g(1,76) > 0$.
Cela signifie que la solution de $g(x) = 0$ est dans l'intervalle ]1,75;1,76[.
Son arrondi à 10⁻¹ est donc 1,8.

2. Le bénéfice (en millions d'euros) d'une grande aciérie en fonction de la quantité $x$ (en tonnes) de métal vendue est donné par la fonction $g$.

a. Quelle quantité minimale doit vendre l'aciérie pour réaliser un bénéfice ?
Corrigé

D'après les questions précédentes, $g(1,8) = 0$ (environ) donc l'aciérie doit produire au moins 1,8 tonnes pour être rentable.

b. Quel est le bénéfice maximal ? Pour quelle quantité de métal vendu ?
Corrigé

D'après le tableau de variation, le bénéfice maximal est (en millions d'euros) \[\frac 1 2 \mathrm e + 3 \approx 4,36.\] Il est atteint pour $\frac 5 2 = 2,5$ tonnes de métal vendu.

retour

code : 550