retour

Soit $f$ la fonction définie sur $]-\infty;-2[\cup]-2;2[\cup]2;+\infty[$ dont la courbe représentative $\mathscr C$ est donnée ci-dessous.

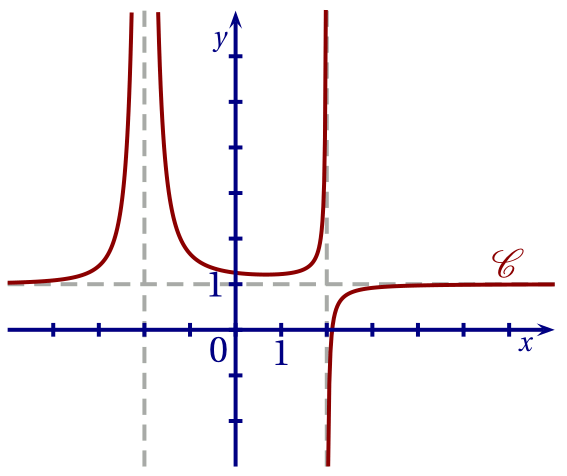
Les asymptotes à $\mathscr C$ sont représentées en pointillés.

1. Donner les équations de ces trois asymptotes.
   Corrigé
   L'asymptote horizontale a pour équation $y = 1$ et les asymptotes verticales ont pour équations $y=-2$ et $y=2$.
2. Lire graphiquement les limites de $f$ aux bornes de son ensemble de définition.
   Corrigé
   Limites: \[\begin{aligned} \lim_{x\to\pm\infty} f(x) &= 1\;;& \\ \lim_{x\to -2} f(x) &= +\infty\;;& \\ \lim_{x\to 2^-} f(x)&=+\infty\;;& \\ \lim_{x\to 2^+} f(x)&=-\infty.& \end{aligned}\]

retour

code : 578