retour

On donne ci-dessous la courbe $\mathscr C_f$, représentative d'une fonction $f$ définie sur $[-3;6]$.
On a aussi représenté les tangentes à $\mathscr C_f$ en certains de ses points.

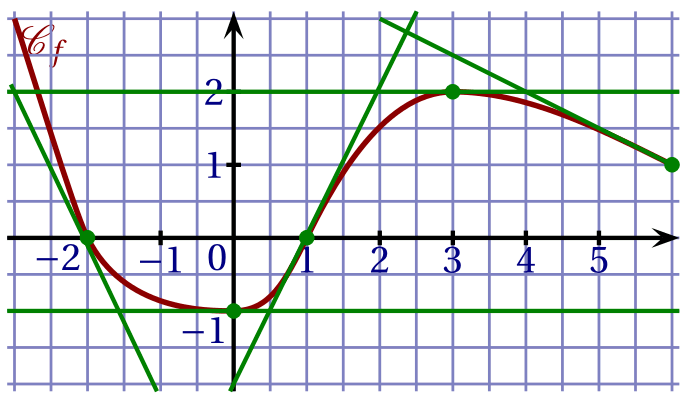
On répondra aux questions suivantes par lecture graphique. Aucune justification n'est demandée.

1. 1. $f(-2)$ et $f'(-2)$; Corrigé
      $f(-2)$ est l'ordonnée du point de $\mathscr C_f$ d'abscisse $-2$. Donc \[f(-2) = 0.\] $f'(-2)$ est le coefficient directeur de la tangente à $\mathscr C_f$ au point d'abscisse $-2$. Donc \[f'(-2) = -2.\]
   2. $f(0)$ et $f'(0)$; Corrigé
      \[f(0) = -1 \quad\text{et}\quad f'(0) = 0.\]
   3. $f(1)$ et $f'(1)$; Corrigé
      \[f(1) = 0 \quad\text{et}\quad f'(1) = 2.\]
   4. $f(3)$ et $f'(3)$; Corrigé
      \[f(3) = 2\quad\text{et}\quad f'(3) = 0.\]
   5. $f(6)$ et $f'(6)$. Corrigé
      \[f(6) = 1\quad\text{et}\quad f'(6) = -\frac 1 2.\]
2. Donner l'ensemble solution de l'inéquation $f(x) \geqslant 0$.
   Corrigé
   Les solutions de l'inéquation $f(x)\geqslant 0$ sont les abscisses des points de $\mathscr C_f$ situés au dessus de l'axe des abscisses. \[S = [-3\;;\;-2]\cup[1\;;\;6].\]
3. Donner l'ensemble solution de l'inéquation $f'(x) \geqslant 0$.
   Corrigé
   Les solutions de l'inéquation $f'(x)\geqslant 0$ forment l'intervalle sur lequel la fonction $f$ est croissante. \[S = [0\;;\;3].\]

retour

code : 595