retour

On définit la suite $(S_n)$ par : \[\forall n\in\mathbb N^*,\quad S_n = \sum_{k=1}^n (2k-1) = 1 + 3 + 5 + \cdots + (2n - 1)\]

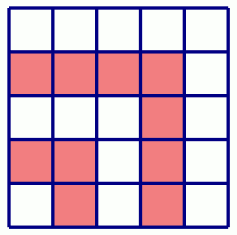
1. En s'aidant éventuellement de la figure ci-contre, conjecturer l'expression de $S_n$ en fonction de $n$.
   Corrigé
   La figure suggère que \[1+3+5+7+9 = 5^2 \iff 1 + 3 + (2\times 5 - 1) = 5^2\] On peut donc conjecturer que $S_n = n^2$.
2. Démontrer la conjecture proposée à la question précédente.
   Corrigé
   Démontrons la conjecture $A(n)$ «$S_n = n^2$» par récurrence.

   • (Initialisation.) $A(1)$ est vraie car $1=1^2$.
   • Si $A(n)$ est vraie, alors \[S_n = 1 + 3 + \cdots + (2n-1) = n^2\] Mais alors : \[\begin{aligned} S_{n+1} &= S_n + \left(2(n+1) - 1\right)& \\ &= n^2 + 2n +2 - 1& \\ &= n^2 + 2n + 1& \\ &= (n+1)^2.& \end{aligned}\] On a donc bien \[\forall n\in\mathbb N^*,\quad A(n) \implies A(n+1).\]

   On en conclut que pour tout entier naturel $n$ non nul, $S_n = n^2$.

retour

code : 7