EX-02
retour
En utilisant la calculatrice, conjecturer la limite en $+\infty$ et $-\infty$ des fonctions suivantes.
a.
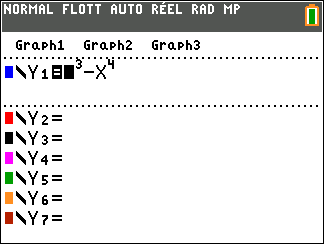
$f:x\mapsto x^3 - x^4$;
Corrigé
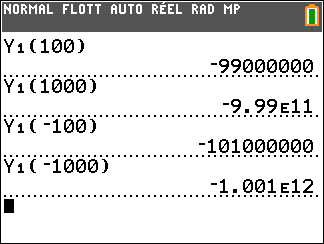
$f(-100) = -1,01\times 10^8$, $f(-1000) \approx -1\times 10^{12}$. On peut conjecturer que
\[\displaystyle\lim_{x\to -\infty} f(x) = -\infty.\]
$f(100) = -9,9\times 10^{7}$, $f(1000) \approx -9,99\times 10^{11}$ On peut conjecturer que
\[\displaystyle\lim_{x\to +\infty} f(x) = -\infty.\]


b.
$g:x\mapsto \dfrac{5x + 3}{x - 8}$.
Corrigé
$g(-100) \approx 4,602$, $g(-1000) \approx 4,957$, $g(-10000)\approx 4,9957$. On peut conjecturer que
\[\displaystyle\lim_{x\to -\infty} g(x) = 5.\]
$g(100)\approx 5,467$, $g(1000) \approx 5,043$, $g(10000) \approx 5,004$. On peut conjecturer que
\[\displaystyle\lim_{x\to+\infty}g(x) = 5.\]






retour
code : 778