EX-10
retour
Soit $\varphi$ (phi) la fonction définie sur $\mathbb R$ par : \[\varphi(x) = \frac{ax^2 + bx + c}{x^2 + 1}.\] Cette fonction est représentée ci-dessous.
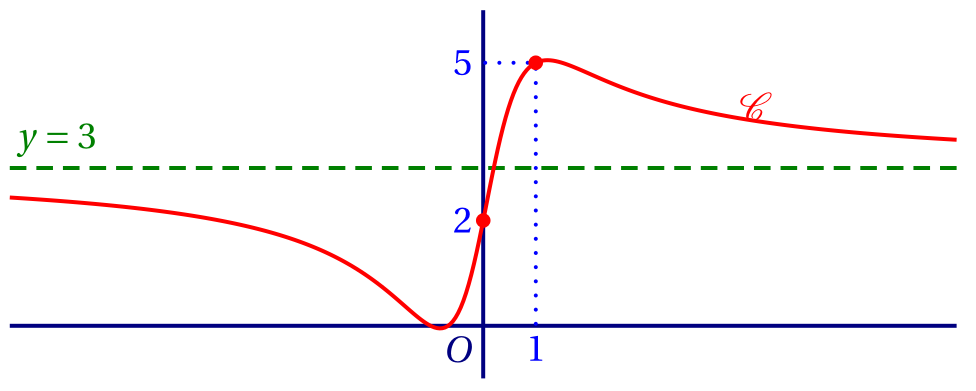
À partir de cette courbe, déterminer les réels $a$, $b$ et $c$, sachant que la droite d'équation $y=3$ est une asymptote à $\mathscr C$ aux infinis.
Corrigé
On a :
\[\varphi(0) = \dfrac{a\times 0^2 + b\times 0 + c}{0^2+1} = c.\]
Or, d'après le graphique, $\varphi(0) = 2$ donc $c = 2$.
Pour tout $x\neq 0$: \[\frac{ax^2+bx+c}{x^2+1} = \frac{x^2\left(a + \frac b x + \frac c {x^2}\right)}{x^2\left(1 + \frac 1 {x^2}\right)}=\frac{a + \frac b x + \frac c {x^2}}{1+\frac 1 {x^2}}.\] Or lorsque $x$ tend vers un infini, les quotients $\dfrac b x$, $\dfrac c {x^2}$ et $\dfrac 1 {x^2}$ tendent vers 0, donc: \[\lim_{x\to +\infty} \varphi(x) = \frac a 1 = a.\] Puisque la droite d'équation $y=3$ est asymptote à la courbe, cette limite est 3, donc $a=3$.
Enfin, on sait que $\varphi(1) = 5$, ce qui équivaut à: \begin{eqnarray*} &\dfrac{3\times 1^2 + b\times 1 + 2}{1^2 +1} = 5&\\ \iff &\dfrac{b+5} 2 = 5&\\ \iff &b +5 = 10&\\ \iff &b = 5.& \end{eqnarray*} Finalement, on a donc pour tout $x\in\mathbb R$: \[\varphi(x) = \dfrac{3x^2 + 5x + 2}{x^2+1}.\]
Pour tout $x\neq 0$: \[\frac{ax^2+bx+c}{x^2+1} = \frac{x^2\left(a + \frac b x + \frac c {x^2}\right)}{x^2\left(1 + \frac 1 {x^2}\right)}=\frac{a + \frac b x + \frac c {x^2}}{1+\frac 1 {x^2}}.\] Or lorsque $x$ tend vers un infini, les quotients $\dfrac b x$, $\dfrac c {x^2}$ et $\dfrac 1 {x^2}$ tendent vers 0, donc: \[\lim_{x\to +\infty} \varphi(x) = \frac a 1 = a.\] Puisque la droite d'équation $y=3$ est asymptote à la courbe, cette limite est 3, donc $a=3$.
Enfin, on sait que $\varphi(1) = 5$, ce qui équivaut à: \begin{eqnarray*} &\dfrac{3\times 1^2 + b\times 1 + 2}{1^2 +1} = 5&\\ \iff &\dfrac{b+5} 2 = 5&\\ \iff &b +5 = 10&\\ \iff &b = 5.& \end{eqnarray*} Finalement, on a donc pour tout $x\in\mathbb R$: \[\varphi(x) = \dfrac{3x^2 + 5x + 2}{x^2+1}.\]
retour
code : 781