EX. 06

retour

1. $f$ est dérivable sur $\mathbb R$ et pour tout réel $x$ : \[f'(x) = 2(2x) - 5\times 1 + 0 = 4x - 5.\] On a: \[\begin{aligned} f'(x) = 0 &\implies 4x - 5 = 0 \implies x= \frac 5 4;&\\ f'(x) > 0 &\implies 4x - 5 > 0 \implies x > \frac 5 4.& \end{aligned}\] D'où le tableau de variation : \[\begin{array}{|c|lcccr|}\hline \rule[-.5em]{0pt}{1.6em}x &-\infty &\quad&\frac 5 4&\quad&+\infty \\ \hline f'(x) &&-&0&+&\\ \hline f(x) &&\searrow& &\nearrow&\\ & & &-\frac{35} 8 & & \\ \hline \end{array} \] Avec : \[f\left(\dfrac{5} 4\right) = 2\left(\dfrac 5 4\right)^2 - 5\left(\dfrac 5 4\right) + 1 =-\dfrac{35}8.\] Représentation graphique :

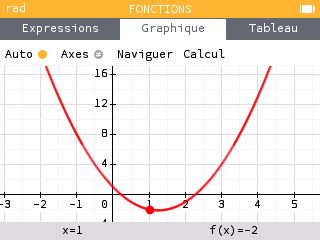
2. La fonction $f$ est dérivable sur $\mathbb R$ et pour tout réel $x$ : \[f'(x) = 3x^2 + 4.\] Puisqu'un carré est toujours positif, on a: \[\begin{aligned} x^2 &\ge 0& \\ \implies 3x^2&\ge 0& \\ \implies 3x^2 + 4 &\ge 4& \\ \implies 3x^2 + 4 &> 0.& \end{aligned}\] Donc le tableau de variation est: \[\begin{array}{|c|lcr|} \hline x &-\infty&\quad&+\infty\\ \hline f'(x) & &+& \\ \hline f(x) & &\nearrow& \\ \hline \end{array}\] Représentation graphique :

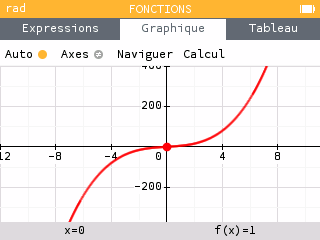
3. La fonction $f$ est dérivable sur $\left]-\infty;\frac 1 5\right[$ et pour tout $x$ de cet intervalle \[f'(x) = \frac{3(5x-1)-53x-1)\times 5}{(5x-1)^2} =\frac 2 {(5x-1)^2}.\] Puisqu'un carré est toujours positif et que pour tout $x$ de cet intervalle $5x-1\neq 0$ : \[\begin{aligned} (5x-1)^2 &> 0& \\ \implies \frac 2 {(5x-1)^2} &> 0& \\ \implies f'(x) &> 0.& \end{aligned}\] $f$ admet donc pour tableau de variation : \[\begin{array}{|c|lcr|}\hline x & -\infty &\qquad &+\infty\\ \hline f'(x) & &+& \\ \hline f(x) & &\nearrow& \\ \hline \end{array}\] Représentation graphique :

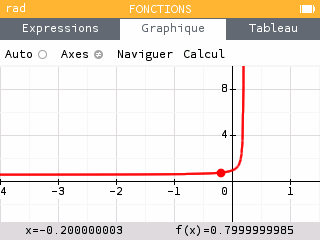
4. Développons l'expression de $f(x)$: \[\begin{aligned} f(x) &= (3x-6)(x^2 - 3x + 2)& \\ &=3x^3 - 9x^2 + 6x - 6x^2 + 18x - 12& \\ &=3x^3 - 15x^2 + 24 x - 12.& \end{aligned}\] On en déduit que pour tout réel $x$ : \[\begin{aligned} f'(x) &= 3(3x^2) - 15(2x) + 24\times 1 - 0& \\ &= 9x^2 - 30x + 24.& \end{aligned}\] Il s'agit d'une fonction polynôme de degré 2 dont on étudie le signe à l'aide du discriminant : \[\Delta = (-30)^2 - 4\times 9 \times 24 = 36.\] Puisque $\Delta > 0$, il y a deux racines : \[\begin{aligned} x_1 &= \frac{30-\sqrt{36}}{2\times 9} = \frac 4 3\;;& \\ x_2 &= \frac{30+\sqrt{36}}{2\times 9} = 2.& \end{aligned}\] $f'(x)$ est du signe de son coefficient principal, $9$, donc positive à l'extérieur des racines.
On a donc le tableau de variation suivant : \[\begin{array}{|c|lcccccr|}\hline x & -\infty &\qquad&\rule[-.5em]{0pt}{1.5em}\frac 4 3&\qquad&2&\qquad&+\infty\\ \hline f'(x) &&{+}&0&-&0&{+}& \\ \hline & & &\rule[-.5em]{0pt}{1.5em}\frac 4 9& & & & \\ f(x) & &\nearrow& &\searrow& &\nearrow& \\ & & & & &0 & & \\ \hline \end{array} \] Représentation graphique :

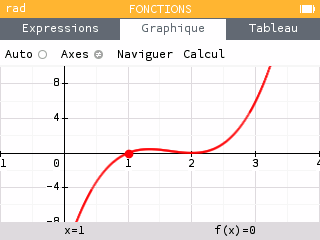
retour

code : 47